5-HMR-0 The NMR Experiment
Nuclear Properties
We are used to thinking of chemical properties in terms of elements (atomic number). For nuclear properties we have to think in terms of isotopes (mass number) - different isotopes of the same element have different nuclear properties. The main nuclear property we are interested in connection with NMR is the nuclear angular momentum spin quantum number I, the "spin" of the nucleus.
I = 0 no spin, the nucleus has no magnetic moment and no NMR properties
I > 0 the nucleus has spin (I = 1/2, 1, 3/2, 2, etc) and a magnetic dipole μ, and thus may be suitable for NMR observation.
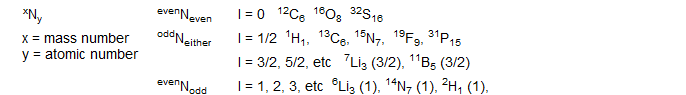
Nuclei with I = 1/2 have especially advantageous NMR properties, and the vast majority of all NMR experiments are done with such isotopes.
Nuclei with I > 0 have angular momentum P (spinning mass) whose direction is the spin axis. The angular momentum is quantized, and can only have one value:
Nuclei with I > 0 also have a magnetic dipole μ (spinning charge). For the NMR experiment it is the ratio of μ to P that matters (much in the way that m/e is what matters in mass spectrometry). We define γ, the gyromagnetic ratio:
Interaction of Nuclei with a Magnetic Field
When we place a nucleus with spin in a magnetic field the nuclei tend to align with the field. The observable component of the angular momentum Pz is also quantized, and can only have the following values:
Quantum restrictions prevent the nuclei from aligning exactly with Bo, since both the angular momentum (P) and the observable component (Pz) are quantized. For spin ½ nuclei there is a tip angle of 54.7°.
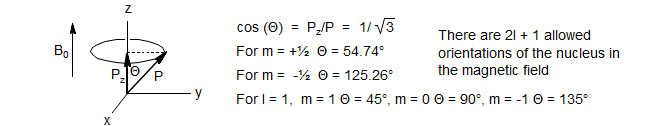
The nuclei precess around the direction of Bo, with a frequency νo (Larmor precession frequency). The frequency is a function of the magnetic field strength (Bo), the angular momentum and the magnetic dipole (Gyromagnetic ratio γ).
Interaction with Radiofrequency
A radiofrequency (at the Larmor precession frequency ν0) applied in the x-direction causes transitions between the spin states if νRF = νo. These transitions are detected by the spectrometer and plotted as an NMR spectrum.
The NMR Spectrometer
An NMR spectrometer consists of a powerful magnet, and the associated electronics to control the properties of the magnet and create and detect radiofrequency signals. In the first spectrometers (up to 60 MHz proton frequency) permanent magnets were used, then electromagnets (to 100 MHz), and now most spectrometers use superconducting magnets to achieve field strengths which give proton resonances from 200 to as high as 900 MHz. The magnetic field must be very stable over a period of hours and very homogeneous over the sample volume (better than 1 part in 109). A complex array of tuning coils is mounted in the magnet and probe to correct for magnetic field inhomogeneities. The radiofrequency generators (at least two are required) must also be very stable, and capable of providing frequencies accurate to 1 part in 109, and with short (microsecond range) very accurately timed pulses. All of these very stringent requirements, together with the inherent insensitivity of the NMR experiment, mean that NMR spectrometers have very complex electronics and are hence the most expensive of all common analytic devices used by chemists, running from $100K to $3M (physicists, of course, use analytic devices that cost billions of dollars).
At the heart of an NMR spectrometer is the probe, which is a removable cylinder inserted into the center of the magnet. The probe contains: the sample tube holder and air spinner outlets; the radiofrequency coils for signal detection, decoupler irradiation, and locking of the magnetic field; the electronics, dewar, gas inlets and outlets for cooling and heating of the sample; the tuning coils for fine adjustments of the magnetic field, as well as (in advanced probes) coils for producing precise field gradients. The very latest probes have the electronics for signal detection cooled to liquid nitrogen or liquid helium temperatures (cryoprobes) to provide substantially improved sensitivity (at a factor of 10 increase in cost). Just an ordinary probe can cost more than a low-end IR or UV spectrometer, and a cryoprobe alone can cost as much as an entire mass spectrometer or X-ray diffraction instrument.
Detection of NMR Signals
The first generation of NMR spectrometers detected the NMR signals in much the same way as was done for the earlier spectroscopic methods such as IR and UV/VIS - the instrument scans through the frequency region of interest (or keeps the frequency constant and scans the magnetic field, a technically easier process used in the first spectrometers). When there is a frequency match (resonance: νRF = νo) the transitions are detected by the coils in the spectrometer probe, and, after signal processing, are plotted as an NMR spectrum.
Advances in microwave electronics made possible a much more efficient way of detecting NMR signals in which frequencies are not scanned, but instead a very short powerful pulse is applied to the sample. The pulse is short enough that its frequency is not well defined to within a few thousand Hertz, so it interacts with all of the nuclei of one isotope in the sample. The pulse duration is accurately specified so that the precession of the nuclei around the axis of the pulse corresponds to a well-defined angle (say 90 degrees).
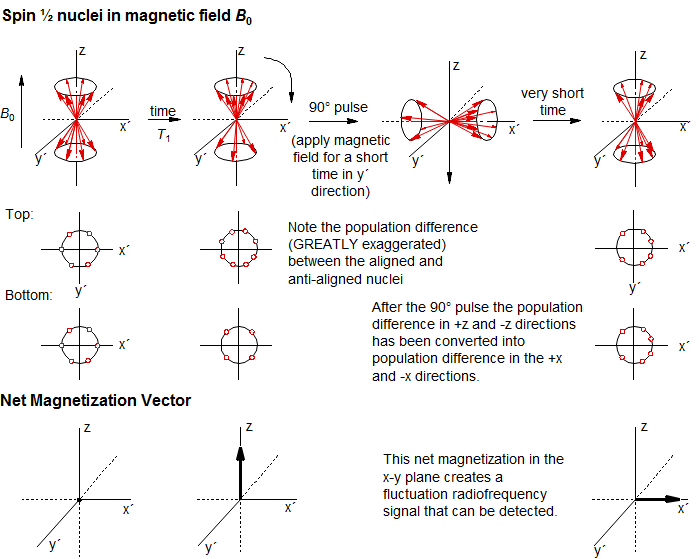
The pulse rotates the excess magnetization (resulting from the higher population of magnetic nuclei in the more stable orientation aligned with the magnetic field Bo) from the z-direction to the x-y plane. This magnetization vector rotates around the x-y plane at the Larmor precession frequency. The fluctuating magnetic field produced by these nuclei is detected by the spectrometer. Each set of nuclei with a distinct chemical shift in the sample has its own precession frequency (the chemical shift), and the spectrometer detects the sum of all of these oscillations (the Free Induction Decay, or FID). The FID is then mathematically manipulated (Fourier transformation) to detect the individual frequencies, which are plotted as a spectrum.
Chemical Shift
Circulation of electrons around the nucleus creates local magnetic fields which shield the nucleus from the external field Bo. The extent of shielding depends on the local chemical environment. Thus NMR signals show a chemical shift. The first NMR spectrometers used continuous wave detection, initially by using a magnetic field sweep to scan through the spectrum (a technically simpler process), later frequency sweep electronics were developed. All modern spectrometers use pulse techniques to detect NMR spectra.
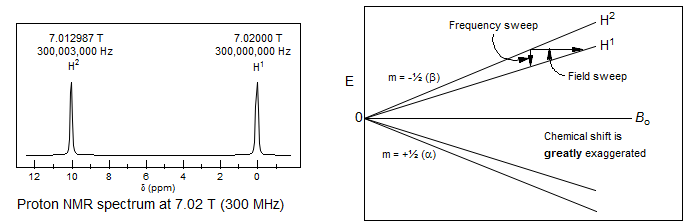
The Larmour precession frequency νo depends on the magnetic field strength. Thus at a magnet strength of 1.41 Tesla protons resonate at a frequency of 60 MHz, at 2.35 Tesla at 100 MHz, and so on. Although Hz are the fundamental energy unit of NMR spectroscopy, the use of Hz has the disadvantage that the position of a peak is dependent on the magnetic field strength. This point is illustrated by the spectra of 2-methyl-2-butanol shown below at several different field strengths, plotted at a constant Hz scale.
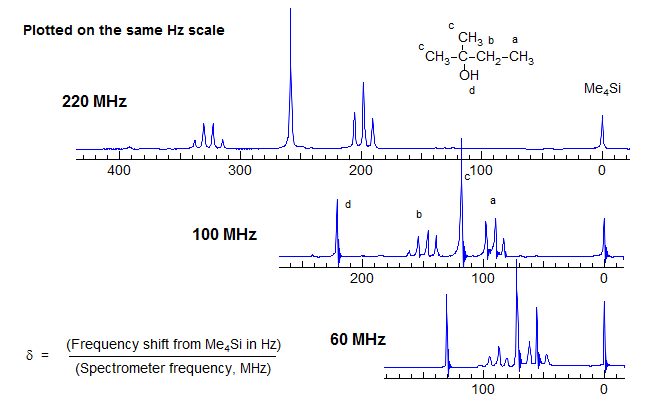
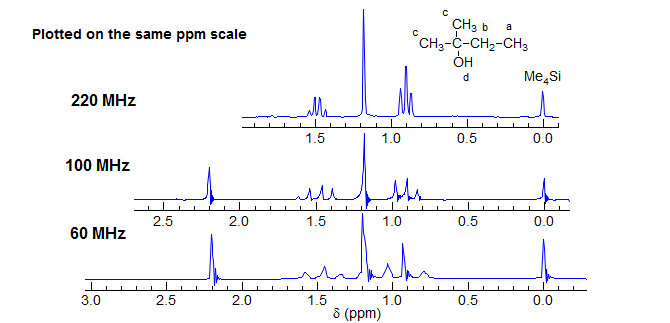
For this reason, the distance between the reference signal (Me4Si) and the position of a specific peak in the spectrum (the chemical shift) is not reported in Hz, but rather in dimensionless units of δ, which is the same on all spectrometers. Note that in the above spectra the multiplet separations (doublet, quartet) are the same at all fields, whereas in the spectra below the chemical shift separations are equal.
Coupling
Neighboring magnetic nuclei can also perturb the local magnetic field, so we observe J-coupling, which causes multiplet structure for NMR signals. J coupling is mutual (JAX = JXA). Coupling constants are independent of the magnetic field, and thus should always be reported in Hz.
Multiplet structure resulting from several couplings to a given nucleus, however, often depends strongly on the chemical shifts between the nuclei, with larger chemical shifts usually leading to simpler spectra. Since chemical shifts (in energy units like Hz) increase with magnetic field strength, higher field magnets typically give much simpler and more easily interpreted NMR spectra. AB, AB2, ABX, ABX3, AA'BB'
Sensitivity
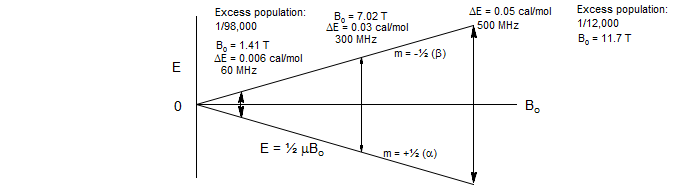
In sharp contrast to UV/VIS/IR spectroscopy, where essentially all molecules are in the ground state at room temperature, in NMR spectroscopy the excited states are thermally populated, with population difference between the spin states of only about one part in 105, so NMR signals are inherently very weak.
The energy separation between the two spin states of a spin ½ nucleus is directly proportional to the strength of the magnetic field (ΔE = μBo). This in turns affects the Boltzmann population differences of the α and β spin states. Thus stronger magnetic fields result in large increases in the strength of the NMR signal.
Relaxation
Relaxation of spin for I = 1/2 nuclei is slow (T1 = 0.1 to 100 sec). This may further weaken NMR signals when the RF field is applied repeatedly (as it usually is), since the population of the spin states can become equalized if nuclei cannot fully relax back to their normal populations between pulses (saturation). See Section 8-TECH-1.
Next Section: Integration · Home