5-HMR-1 Integration of Proton NMR Spectra
NMR is unique among common spectroscopic methods in that signal intensities are directly proportional to the number of nuclei causing the signal (provided certain conditions are met). In other words, all absorption coefficients for a given nucleus are identical. This is why proton NMR spectra are routinely integrated, whereas IR and UV spectra are not. A typical integrated spectrum is shown below, together with an analysis.
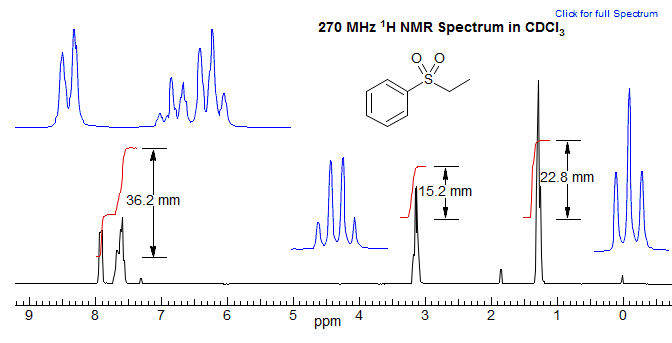
The vertical displacement of the integral gives the relative number of protons It is not possible to determine the absolute numbers without additional information (such as a molecular formula). In the example above, if we add up all of the integrals, we get 74.3. Dividing each integral by the smallest one (15.2) gives a ratio of 2.38/1.0/1.50 for the three signals. Multiplying by two gives 4.76/2.0/3.03, which is close to the integral numbers (5/2/3) expected for a pure compound. However, there is nothing in the spectrum that rules out 10/4/6 or higher multiples. If we have a molecular formula (in this case C8H10O2S), dividing by the number of hydrogens gives 7.4 mm per H. We can then determine the number of protons corresponding to each multiplet by rounding to the nearest integer. It is generally possible to reliably distinguish signals with intensities of 1 to 10 or so, but it becomes progressively harder to make a correct assignment as the number of protons in a multiplet increases beyond 10, because of the inherent inaccuracies in the method.
The two parts of aromatic proton integral at δ 7.6 and 7.9 can be separately measured as a 2:3 ratio of ortho to meta+para protons.
If given the molecular formula (C8H10O2S), we know there are 10H in molecule
Total area: 36.2 + 15.2 + 22.8 = 74.2 mm
Thus 7.4 mm per H
36.2 / 7.4 = 4.89 i.e. 5H
15.2 / 7.4 = 2.05 i.e. 2H
22.8 / 7.4 = 3.08 i.e. 3H
Accuracy of Proton NMR Integrations
The integration of NMR spectra can be carried out with high accuracy, but this is only possible if a number of sources of error are properly handled. On a modern spectrometer accuracy of ±5% can be achieved easily if relaxation issues are handled properly. To get errors of <1% a number of factors have to be considered and optimized.
1. Signal to Noise. The spectrum must have adequate signal to noise to support the level of accuracy required for the experiment.
2. Saturation Effects. NMR spectroscopy has a feature unique among spectroscopic methods, that relaxation processes are relatively slow (on the order of seconds or tenths of seconds), compared to milli, micro, and pico seconds for IR and UV. In other words, once the spectrometer has perturbed the equilibrium population of nuclei by scanning over the resonance frequency or pulsing the nuclei, it takes from 0.1 to 100s of seconds (typically several seconds) for them to return to their original populations (T1 the spin-lattice relaxation time). If power settings are too high (for CW spectra) or pulse angle and repetition rates too high (for FT spectra) then spectra can become saturated, and integrations less accurate, because the relaxation rates of various protons in the sample are different. Saturation effects are particularly severe for small molecules in mobile solvents, because these typically have the longest T1 relaxation times.
To get reliable integrations the NMR spectrum must be acquired in a way that saturation is avoided. It is not possible to tell whether a spectrum was run appropriately simply by inspection, it is up to the operator to take suitable precautions (such as putting in a 5-10 second pulse delay between scans) if optimal integrations are needed. Fortunately, even a proton spectrum taken without pulse delays will usually give reasonably good integrations (say within 10%). It is important to recognize that integration errors caused by saturation effects will depend on the relative relaxation rates of various protons in a molecule. Errors will be larger when different kinds of protons are being compared (such as aromatic CH to a methyl group), than when the protons are similar or identical in type (e.g. two methyl groups).
3. Line Shape Considerations. NMR signals in an ideally tuned instrument are Lorenzian in shape, so the intensity extends for some distance on both sides of the center of the peak. Integrations must be carried out over a sufficiently wide frequency range to capture enough of the peak for the desired level of accuracy. Thus, if the peak width at half height is 1 Hz, then an integration of ±2.3 Hz from the center of the peak is required to capture 90% of the area, ±5.5 Hz for 95%, ±11 Hz for 98% and ±18Hz for >99% of the area. This means that peaks that are closely spaced cannot be accurately integrated by the usual method, but may require line-shape simulations with a program like NUTS or WINDNMR to accurately measure relative peak areas.
4. Digital Resolution. A peak must be defined by an adequate number of points if an accurate integration is to be obtained. The errors introduced are surprisingly small, and reach 1% if a line with a width at half height of 1 Hz is sampled every 0.5 Hz.
5. Isotopic Satellites. All C-H signals have 13C satellites located ±JC-H/2 from the center of the peak (JC-H is typically 115-135 Hz, although numbers over 250 Hz are known) Together these satellites make up 1.1% of the area of the central peak (0.55% each). They must be accounted for if integration at the >99% level of accuracy is desired. Larger errors are introduced if the satellites from a nearby very intense peak fall under the signal being integrated. The simplest method to correct this problem is by 13C decoupling, which compresses the satellites into the central peak. A number of other elements have significant fractions of spin ½ nuclei at natural abundance, and these will also create satellites large enough to interfere with integrations. Most notable are 117/119Sn, 29Si, 77Se, 125Te, 199Hg. For more on satellites, see Section 7, Multinuclear NMR.
There is a bright side to 13C satellites: they can be used as internal standards for the quantitation of very small amounts of isomers or contaminants, since their size relative to the central peak is accurately known.
6. Spinning Sidebands. These can appear at ± the spinning speed in Hz in spectra run on poorly tuned spectrometers and/or with samples in low-quality tubes. They draw intensity from the central peak. SSBs are rarely significant on modern spectrometers.
7. Baseline Slant and Curvature. Under some conditions spectra can show significant distortions of the baseline, which can interfere with obtaining high-quality integrations. Standard NMR work-up programs have routines for baseline adjustment.
8. Decoupling. When decoupling is being used, as is routinely done for 13C NMR spectra and occasionally for 1H NMR spectra, peak intensities are distorted by Nuclear Overhauser Effects (NOE, see Sect. 8). Integrations of such spectra might not give accurate ratios of peak areas.
Peak Intensities. Under certain conditions, peak heights can also be a quite accurate method of quantitation. For example, if several singlets are being compared, and they all have identical line widths, and the spectra were measured such that there are sufficient data points to define the lineshape of each singlet, then peak heights may be useful, and under ideal conditions more accurate than integrations.
Determining Absolute Amounts by NMR Integration. Although NMR spectra in principle follow Beer's law, it is difficult (although not impossible) to make effective use of the absolute intensities of NMR spectra for quantitation (as is routinely done for UV, and sometimes IR). NMR integrations are always relative. Thus an internal standard must be used to determine reaction yields by NMR integration. A commonly used internal standard for proton NMR spectra is pentachloroethane -- it is a liquid, not too volatile, and appears in a region of the NMR spectrum (δ 6.11) where there are few signals. It is strongly recommended to avoid using volatile materials like CH2Cl2, CHCl3, C6H6 and others, since it is very difficult to avoid some evaporation losses during the transfer process of the standard, leading to incorrect (high) concentrations of the substrate.
Next Section: Chemical shifts · Previous Section: NMR Experiment · Home