5-HMR-3 Spin-Spin Splitting: J-Coupling
There are two distinct types of magnetic interaction (coupling) between nuclei (A and X) with a non-zero spin - the direct interaction (dipole-dipole coupling: D) and the indirect or scalar coupling (spin-spin splitting: J). The direct interaction is about 1000 times as large as the scalar coupling (e.g. at 2 Å distance H-H dipolar coupling is ca 30,000 Hz). These direct couplings make the observation of high-resolution NMR spectra in solids and very viscous liquids difficult, and make NMR spectra in liquid crystals (where molecules are partially oriented, and the dipolar coupling is only partially averaged) very complex. In mobile isotropic liquids the random motion of molecules completely averages the dipolar coupling, so no direct effects are seen. There are however, indirect effects, such as the Nuclear Overhauser Effect (NOE) which have important consequences for NMR spectroscopy (see Sect. 8). In the following sections we will be concerned only with J coupling.
The scalar coupling J is a through-bond interaction, in which the spin of one nucleus perturbs (polarizes) the spins of the intervening electrons, and the energy levels of neighboring magnetic nuclei are in turn perturbed by the polarized electrons. This leads to a lowering of the energy of the neighboring nucleus when the perturbing nucleus has one spin, and a raising of the energy whenwhen it has the other spin. The J coupling (always reported in Hz) is field-independent (i.e. J is constant at different external magnetic field strength), and is mutual (i.e. JAX = JXA). Because the effect is usually transmitted through the bonding electrons, the magnitude of J falls off rapidly as the number of intervening bonds increases. Coupling over one (1J), two (2J) and three (3J) bonds usually dominates the fine structure of NMR spectra, but coupling across four and five (4J, 5J) bonds is often seen, especially through π bonds (double and triple bonds, aromatic carbons).
5-HMR-3.1 Sign of Coupling Constants
Coupling constants can be either positive or negative, defined as follows: coupling constants are positive if the energy of A is lower when X has the opposite spin as A (αβ or βα), and negative if the energy of A is lower when X has the same spin as A (αα or ββ).

Mechanism of spin polarization: It is known from spectroscopy of the hydrogen radical (H·) that the more stable orientation has the angular momentum vectors of the nucleus and the electron antiparallel. Since the gyromagnetic ratio of the nucleus is positive, and that of the electron is negative, this means that the magnetic vectors are parallel.

For the Fermi contact mechanism of spin-spin coupling (there are other mechanisms), the bonding electrons for a H-13C fragment will become polarized as shown, so that the more stable orientation of the 13C-nucleus will be down, when the proton is up. This corresponds to a positive one-bond C-H coupling.
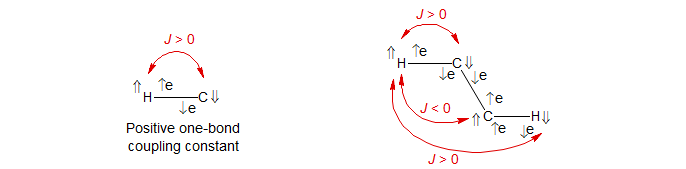
If we continue down the bond sequence, the polarization of the C-H electrons will cause polarization of the C-C electron pair. Again, parallel spins are the more stable orientation (triplets are more stable than singlets -- Hund's rule). Thus the two-bond coupling (2J) is predicted to be negative, and the three-bond coupling (3J) positive. This alternation of signs is often (but by no means always) seen.
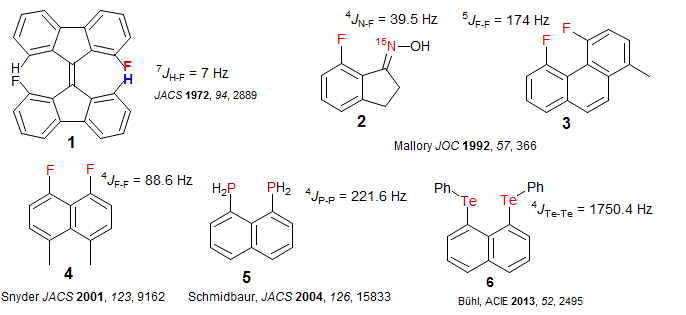
Through-Space Coupling. The principal mechanism for J-coupling is through bond polarization, but there are situations where a through-space effect seems to be operative. These occur in molecules where spin 1/2 nuclei are forced into close proximity. For example, in compound 1 below, there is a substantial H - F J coupling even though the H and F are separated by seven bonds, where normally coupling is small or undetectable. Other examples thought to involve significant through space 15N-F (2), F-F (3, 4) and P-P (5) coupling are shown.
Much larger through-space coupling can be seen for heavier elements, for example between 123Te and 125Te in 1,8-bisphenyltelluro naphthalene (6).
A depiction of the perturbation of energy levels of a nucleus A by a neighboring magnetic nucleus X is shown below (spin-spin splitting). The principal magnetic nuclei are other protons, the 100% abundant spin ½ nuclei 19F and 31P, and some spin 1 or greater (quadrupolar) nuclei such as 14N, 2H, 11B, and 12B. Although Br, Cl, and I all have isotopes with spin >½, coupling is not seen because of relaxation effects. This will be discussed in more detail in Section 7.
5-HMR-3.2 Two Different Couplings to one Proton
Consider the NMR spectrum of 3,4-dichlorobenzoyl chloride below.
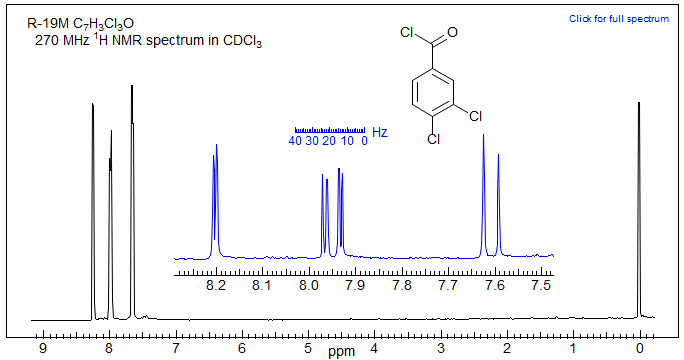
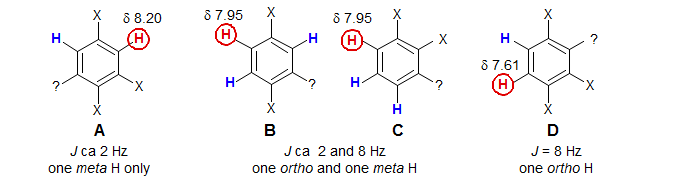
The proton-proton couplings in benzene are typically 7-9 Hz for Jortho, 2-3 Hz for Jmeta and <1 Hz for Jpara. The substitution pattern can be derived from examination of each of the three aromatic protons. For example, the doublet at δ 8.2 with J = 2.5 Hz is interpreted as follows: this proton has no protons ortho to it, and only one proton meta to it. Structure A summarizes the information. For the doublet of doublets at δ 7.95 (J = 8.5, 2.3 Hz), formed by coupling of one proton to both an ortho and a meta proton, the two structures B and C are possible. The doublet at δ 7.6 (J = 8.5 Hz) defines the substitution pattern of structure D. In each case the position marked by ? is undefined since the para coupling is usually too small to resolve.
A slightly more complicated case is 1,1,2-trichloropropane. A simulated (WINDNMR) spectrum is shown below.
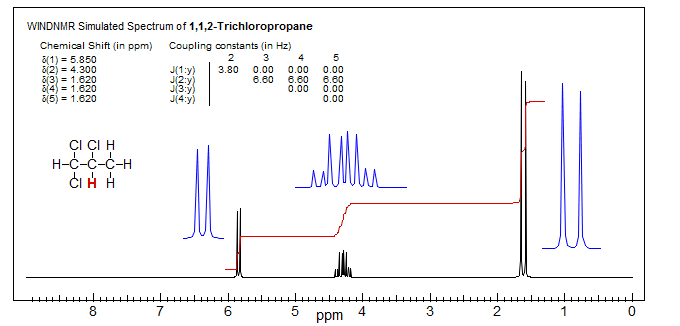
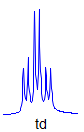
The C-2 proton is coupled to one proton at C-1 and three protons of the methyl group at C-3. Naively, one might expect a pentet (p), as shown in the left spectrum below. Although pentets are, in fact, often observed in such situations, this occurs only if J1-2 and J2-3 are identical. When they are not (as is actually the case in this example), then we get a quartet of doublets (qd). It is customary to quote the larger coupling first (q) and then the smaller coupling (d). A proper text description of the multiplet is: δ 4.30, 1H, qd, J = 6.6, 3.8 Hz.
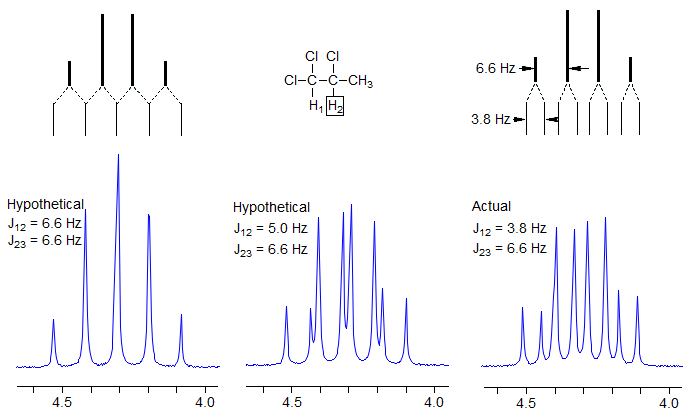
Exercise: what would a dq, J = 6.6, 3.8 Hz look like?
5-HMR-3.3 First Order Coupling Rules
1. Nuclei must be chemical shift nonequivalent to show obvious coupling to each other. Thus the protons of CH2Cl2, Si(CH3)4, Cl-CH2-CH2-Cl, H2C=CH2 and benzene are all singlets. Equivalent protons are still coupled to each other, but the spectra do not show it. There are important exceptions to this rule: the coupling between shift equivalent but magnetically inequivalent nuclei can have profound effects on NMR spectra - see Sect. 5.7
2. J coupling is mutual, i.e. JAB = JBA always. Thus there is never just one nucleus which shows J splitting - there must be two, and they must have the same splitting constant J. However, both nuclei need not be protons - fluorine (19F) and phosphorus (31P) are two other common nuclei that have spin ½ and 100% abundance, so they will couple to all nearby protons (the other 100% spin 1/2 nuclei are 89Y, 103Rh and 169Tm). If these nuclei are present in a molecule, there are likely to be splittings which are present in only one proton multiplet (i.e. not shared by two multiplets).
3. Two closely spaced lines can be either chemically shifted or coupled. It is not always possible to distinguish J from δ by the appearance of the spectrum (see Item 4 below). For tough cases (e.g. two closely spaced singlets in the methyl region) there are several possibilities:
· decouple the spectrum
· obtain it at a different field strength (measured in Hz, coupling constants are field independent, chemical shifts are proportional to the magnetic field)
· measure the spectrum in a different solvent - benzene and chloroform are a good pair of solvents (chemical shifts are usually more solvent dependent than coupling constants).
For multiplets with more than two lines, areas, intensities, symmetry of the pattern and spacing of the lines generally make it easy to distinguish chemical shift from coupling.
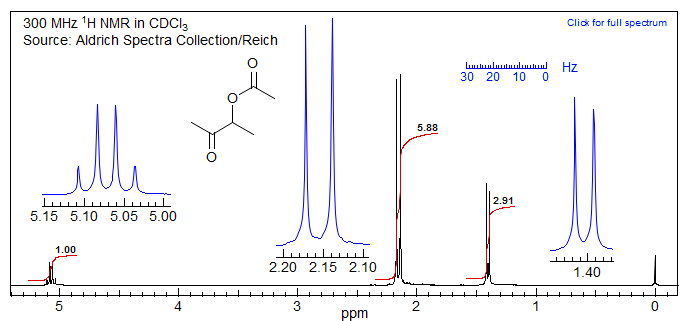
For a simple example see the spectrum of 3-acetoxy-2-butanone below. Here it is pretty easy to identify one of the doublets as the 4-methyl group, the other "doublet" (with a separation of 9 Hz, which could easily be a coupling) actually corresponds to the two CH3C(=O) groups.
4. Chemical shifts are usually reported in δ (units: ppm) so that the numeric values will not depend on the spectrometer frequency (field-independent units), coupling constants are always reported in Hz (cycles per second). Chemical shifts are caused by the magnetic field, couplings are field-independent, the coupling is inherent in the magnetic properties of the molecule. However, all calculations on NMR spectra are done using Hz (or, more precisely, radians per sec).
5. Protons two (2J, geminal) or three bonds (3J, vicinal) apart are usually coupled to each other, more remote protons (4J, 5J) may be if geometry is right, or if π-systems (multiple bonds) intervene. Long range couplings (4J or greater) are usually small, typically <0.5 Hz, but up to 3 Hz in some cases where there are intervening π bonds.

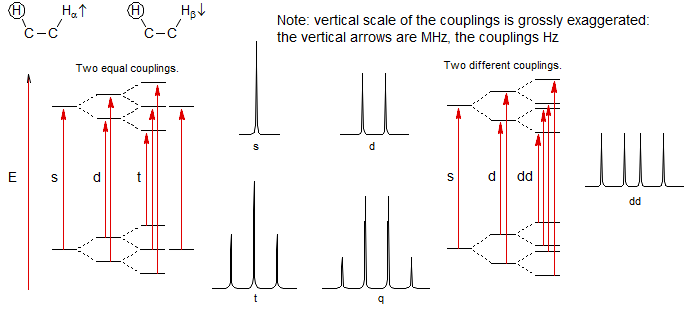
6. Multiplicity for first order patterns follows the "doubling rule". If all couplings to a particular proton are the same there will be 2nI+1 lines, where I is the spin and n is the number of neighboring nuclei (n + 1 for 1H I = 1/2). The intensities will follow Pascal's triangle.
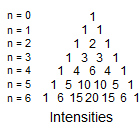
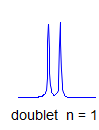
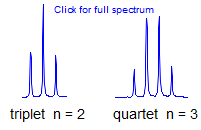
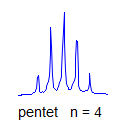
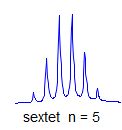
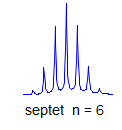
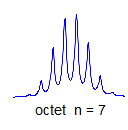
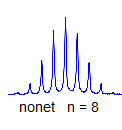
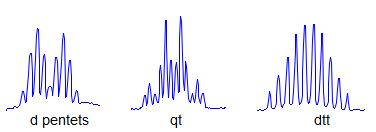
7. If all couplings are different, then the number of peaks is 2n for 1H, and the intensities are 1:1:1: . . .. Thus a proton coupled to two others by different couplings gives a dd (doublet of doublets, see Figure). This pattern is never called a quartet. As the number of couplings gets larger, accidental superpositions of lines will sometimes occur, so that the 1:1:1... intensity ratio no longer applies. The intensities are also often distorted by leaning effects (see AB/AX patterns), as seen in a couple of the examples below.
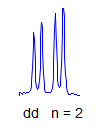
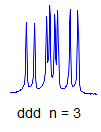
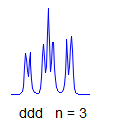
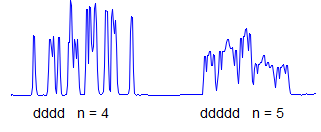
8. More typically, some of the couplings are the same, others different, so get a variety of patterns. In favorable cases, these patterns can be analyzed and all couplings extracted. The number and size of couplings (J-values) provide important structural information.
Second Order Effects
Protons or groups of protons form simple multiplets only if the chemical shift differences between the protons (Δν) are large compared to the coupling constants between them (J). If Δν/J (all in Hz) is <5 then second order effects appear (see 5-HMR-9) which complicate the analysis.
Rules for Analyzing First Order Multiplets
A first order multiplet can be expected when both of the following criteria are met:
First, the chemical shift of the observed proton must be far away from any of the protons it is coupled to (far away means Δν >> J). In practice, multiplets can be treated in a first order fashion if Δν > 3J, although the substantial leaning distortions can complicate analysis. The leaning will have almost completely disappeared by the time Δν = 10J.
Second, if more than one proton is coupled to the observed one, then these protons must not be "strongly coupled." In other words, if they are coupled to each other and very close in chemical shift then the observed proton multiplet may not yield true coupling constants on analysis, even though it looks first order. See the section on Virtual Coupling.
Structure of First Order Multiplets. The fundamental rule governing multiplet intensities for spin 1/2 nuclei with all couplings identical is Pascal's triangle (n = number of equivalent couplings). A very characteristic and diagnostic intensity relationship is that between the first and second lines - the intensity ratio is 1/n, where n is the number of equivalent coupling partners.

A first order multiplet consists of the product (not the sum) of several such multiplets. In other words, a single line will first be split into one of the symmetrical multiplets (1:1 d, 1:2:1 t, 1:3:3:1 q, etc), then each line of this multiplet will be again split into d, t, q, or higher multiplet.
1. All truly first order multiplets are centrosymmetric - there is a mirror plane in the middle (in real spectra, this is usually not strictly true because of leaning and other distortions). However, the reverse is not true: not all symmetrical multiplets are first order.
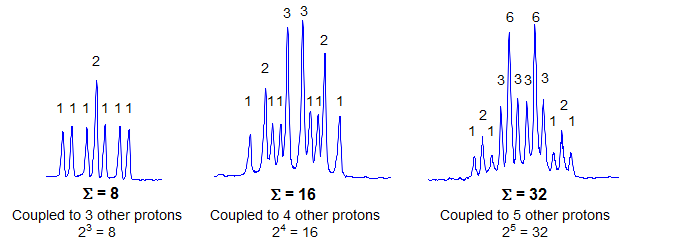
2. If the small outermost peaks are assigned intensity 1, then all other peaks must be an integral multiple intensity of this one (1x, 2x, 3x, 4x in height), and the total intensity of all peaks must be a power of 2 (2, 4, 8, 16, 32, etc). The intensity of each of the two outermost lines is 1/2n of the total multiplet intensity, where n is the number of protons which are coupled with the proton signal being analyzed. There can be no lines smaller than the outermost one. Note, however, that if n is large, the outermost peaks may not be distinguishable from noise. Intensity assignments and determination of n cannot be easily made for such multiplets
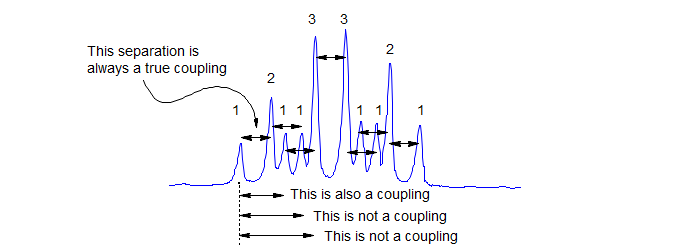
3. There is a strict regularity of spacing in a first order multiplet: if you have correctly identified a coupling constant J, then every peak in the multiplet must have a partner J Hz away to the left or to the right of it.
4. Most first order multiplets integrate to a single proton, a few may be 2 or 3 protons in area. It is rare to have more than 3 protons, unless there is symmetry in the molecule (e.g., (CH3)2CH- gives a 6-proton doublet for the methyl groups). Thus a 4-proton symmetrical multiplet is usually not a first-order pattern (it is more likely to be the very common AA'BB' pattern).
5. The symmetry and intensities of an otherwise first-order multiplet can be distorted by leaning effects (see Section 5-HMR-9). Many such multiplets can still be correctly analyzed by first-order techniques, but you have to mentally correct for the intensity distortions. However, the coupling constants extracted may not be perfectly accurate.
5-HMR-3.5 Analyzing a First Order Multiplet
First order multiplets are analyzed by constructing a reverse coupling tree, by "removing" each of the couplings in turn, starting with the smallest.
1. "Take out" the smallest couplings first. The separation between the two lines at the edge of the multiplet is the smallest coupling. Each time you remove a coupling you generate a new, simpler multiplet, which can then be analyzed in turn. Remember that each line of the multiplet participates in each coupling.
2. Watch line intensities (i.e., peak areas or peak heights) carefully--when you "take out" a coupling, the intensities of the newly created lines should be appropriate (i.e., each time you "take out" a coupling, also "take out" the proper intensity). When a coupling has been taken out completely, all intensity should be accounted for. Keep track of your analysis by using a "coupling tree".
3. The couplings may be removed one at a time as doublets, or as triplets, quartets and higher multiplets. The intensity ratio of the first two lines signals the number of protons involved in the coupling: 1:1 means there is only one proton, 1:2 means that there are 2 protons (triplet), etc. Be especially careful to keep track of intensities when you "take out" triplets (1:2:1) or quartets (1:3:3:1). Each time you completely remove a coupling you generate a new simpler multiplet which follows first order rules, and can be analyzed in turn.
When you have finished your analysis, all peaks and all intensity in the multiplet must be accounted for. You can check the analysis as follows: the separation of the two outermost peaks of the multiplet is the sum of all the J's (i.e., for a dt, J = 8, 3 Hz the outermost lines are separated by 8 + 3 + 3 = 14 Hz).
Here are two multiplets analyzed using this technique:
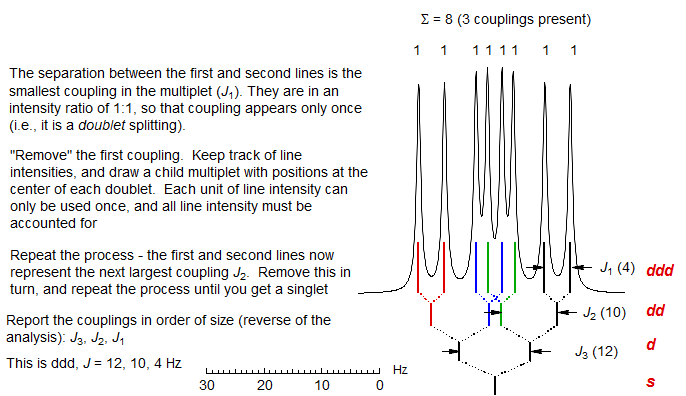
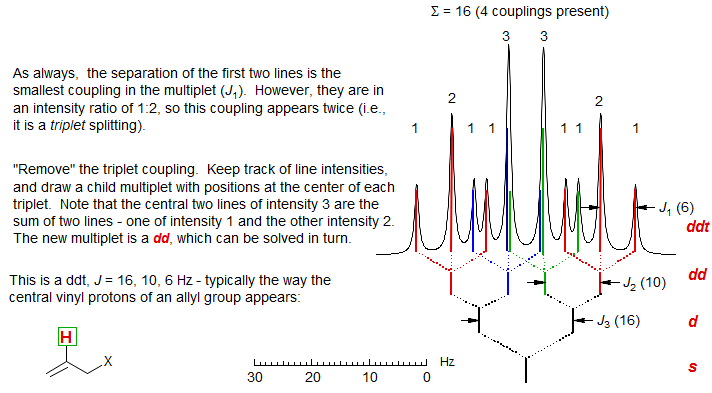
Reporting a First Order Multiplet. Multiplets are reported starting with the largest coupling, and the symbols must be in the order of the reported numbers: δ 2.10, 1H, qt, J = 10, 6 Hz means: a single proton q of 10 Hz, t of 6 Hz with a chemical shifts of 2.10 ppm.
Quartets. Keep clear in your mind the distinction between a simple q (one proton equally coupled to 3 others, with an intensity 1:3:3:1), an ABq (2 protons coupled to each other, see Section 5-HMR-10), and the quartet formed by coupling with a spin 3/2 nucleus (e.g., 7Li, intensity 1:1:1:1, see Sect 7-MULTI-2). Only the first of these should be referred to by just a "q" symbol. The early NMR literature (and even modern novices) sometimes call doublets of doublets "quartets" (there are four lines, after all). Don't do this.
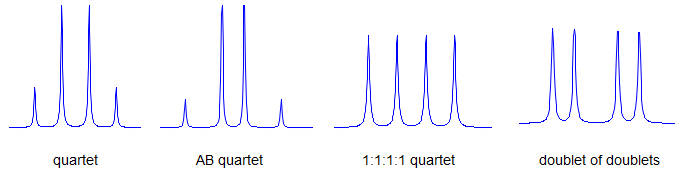
Practice Multiplets
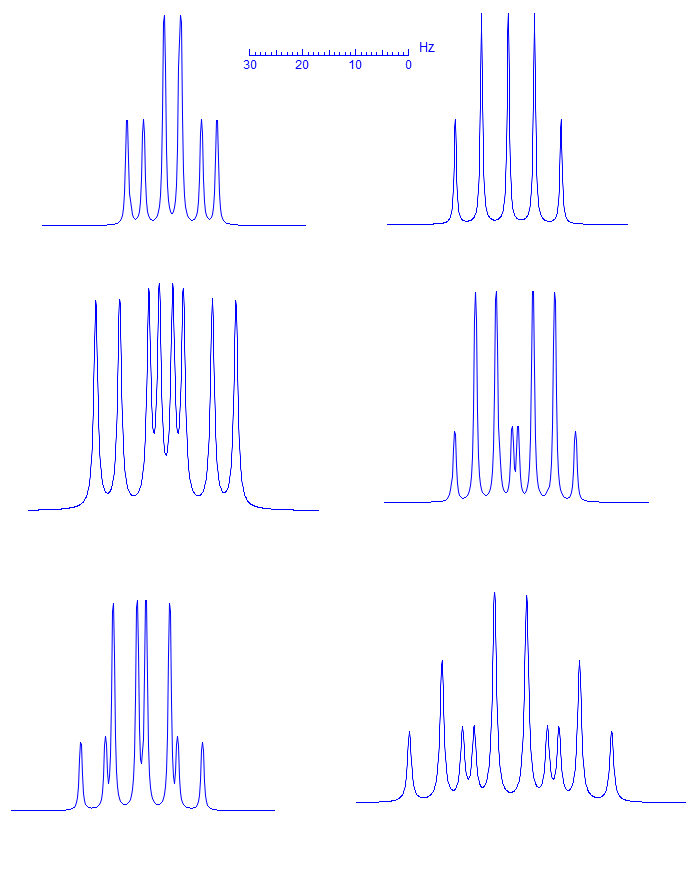
5-HMR-3.6 First Order Multiplets
Exercise: Assign the protons shown, and identify the various couplings. Note the leaning in many of the multiplets, indicating that the coupled partner is not too far away.
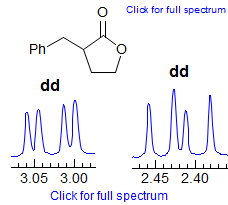
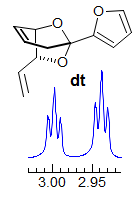
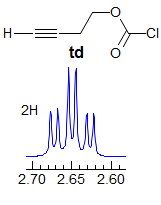
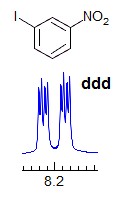
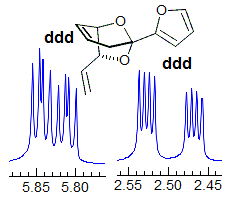
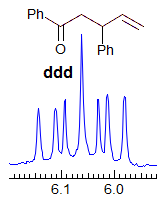
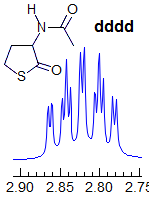
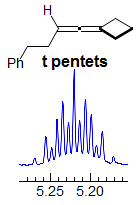
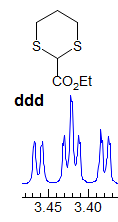
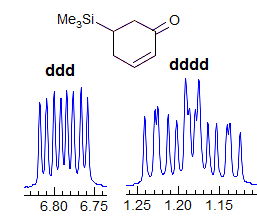
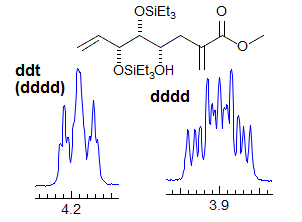
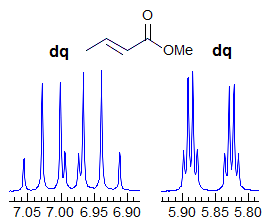
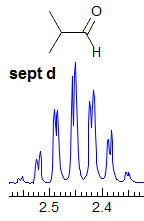
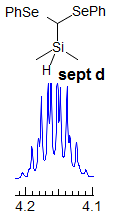
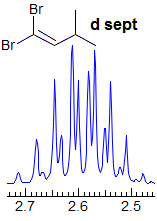
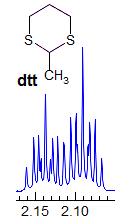
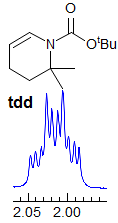
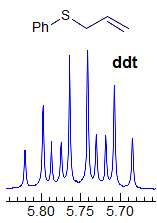
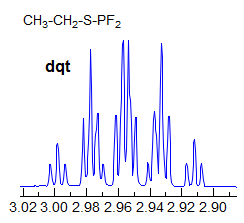
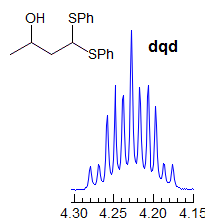
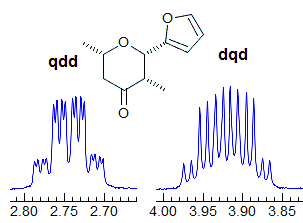
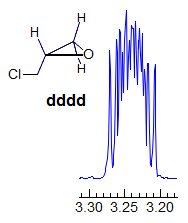
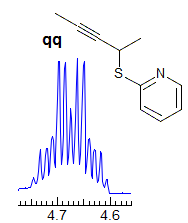
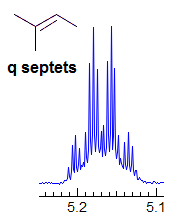
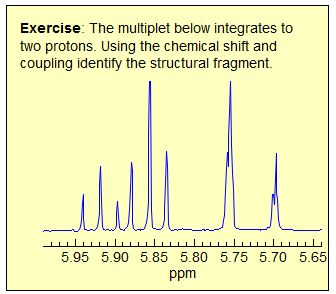
5-HMR-3.7 Symmetrical Multiplets which are NOT First Order
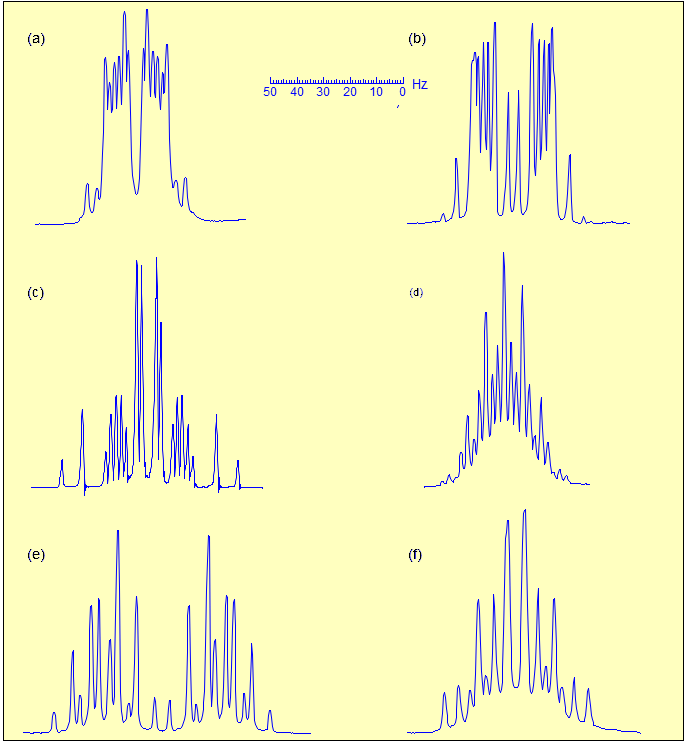
Exercise: Only ONE of the multiplets below is first order, find it. A second one is almost first order, but ultimately can be ruled out because of a very subtle line position inconsistency.
Some criteria to use:
· Pattern must be centrosymmetric (true of all of these)
· Intensity of lines - patterns must be repeated, especially examine outer lines
· Be wary if #H > 1, especially if 4H
· Consider size of possible couplings
5-HMR-3.8 Accidental Coincidence of Coupling Constants in First Order Spectra
True higher order coupling patterns (t, q, pentet, septet, etc) result from two, three, four or more symmetry-equivalent couplings to one proton. Such multiplets also arise from the accidental equivalence of two or more different couplings.
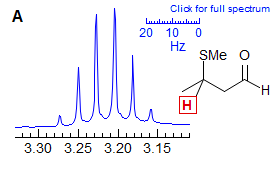
An illustrative example is the multiplet in spectrum A, which corresponds to the proton α to the MeS group. We know that there must be three different couplings here: to the CH3 group, which would give a true quartet, and to the diastereotopic CH2 protons, each should give a doublet splitting, so technically this is a qdd, Yet this looks like a perfect sextet - clearly all three couplings are close to identical. There has been some controversy in this area as to how to report such multiplets - do we call this a qdd or a sextet? Here we have chosen the "what you see is what you report" option and called it a sextet. Nearly equal couplings to chemically different protons are commonly seen in acyclic sp3 chains of atoms (propyl groups, isobutyl groups, etc). It might sometimes be advisable, particularly in strongly misleading situations, to call this an apparent sextet in A, or an apparent qd in B to indicate there is more here than meets the eye.
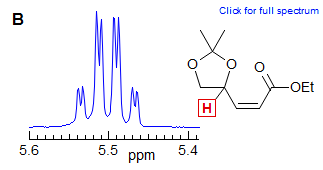
The gem (2J) and axial-axial (3J) coupling in chair cyclohexanes and 6-membered heterocycles are often very similar in magnitude, although with opposite signs (not relevant in first order spectra), leading to apparent triplets, as in Spectrum C, or quartets, as in D.
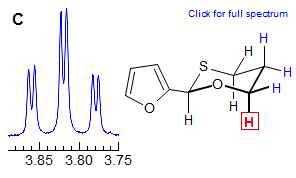
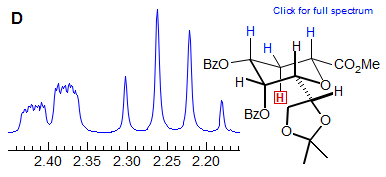
The axial-equatorial and equatorial-equatorial 3J coupling in cyclohexanes are also often similar in size, leading to apparant triplet splittings (dt in Spectrum E, dtd in F). Note that in E the middle peak of the triplets are somewhat broader indicating a small difference in the two couplings, at higher resolution we might see a ddd. Spectrum F also shows an ax/ax gem near coincidence (qd at 2.05).
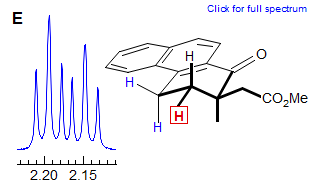
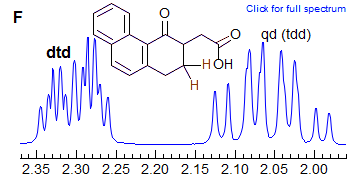
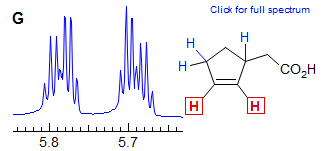
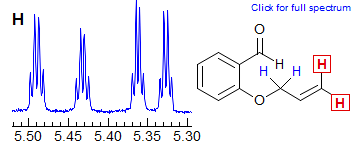
In cyclopentenes, the vicinal and four bond allylic couplings 3J and 4J) are often very similar, as seen in Spectrum G, where both vinyl protons are apparent dq, even though each quartet clearly must involve three different J values. Another common coincidence derives from the similarity in vinyl gem coupling (2J) and long-range allylic coupling 4J, as in Spectrum H, where both terminal vinyl protons are dq.
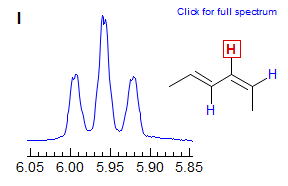
Other common equivalent couplings are seen in the nearly identical ca 10 Hz coupling of the central protons in conjugated dienes, and coupling to cis protons across the double bond, as seen in Spectrum I. Another Example: 1.
5-HMR-3.9 Measurement of Coupling Constants
The accurate measurement of J coupling constants requires that multiplets be correctly analyzed. In the following pages are described techniques for performing such analyses.
For first order multiplets a simple "coupling tree" analysis as described in Section 5-HMR-3.9 can directly yield coupling constants within the accuracy of the digital resolution of the spectrum. This includes AB spectra, where JAB can be measured directly. See Section 5-HMR-7 for a description of the ABC... (Pople) nomenclature for spin systems.
For AB2 spectra both the coupling constant JAB and the chemical shifts can be obtained by simple arithmetic manipulations, provided that line assignments can be made correctly. For ABX spectra JAB is accurately measureable by inspection. An approximate analysis, which treats the peaks as AMX, will give values for JAX and JBX that will be in error by varying amounts, depending on the relative size of JAB and νAB (the smaller νAB the larger the error), and the relative size of JAX and JBX. To get accurate values for the JAX and JBX coupling constants a proper ABX analysis as described in Section 5-HMR-12 is required.
Coupling Between Homotopic and enantiotopic protons. For many simple compounds the symmetry is such that protons are homotopic or enantiotopic, and no coupling constants can be measured directly (e.g., the 2J coupling in methane or dichloromethane; the ortho, meta, and para couplings in benzene; the cis, trans and gem couplings in ethylene, etc). For such compounds the following techniques are used to measure JHH:
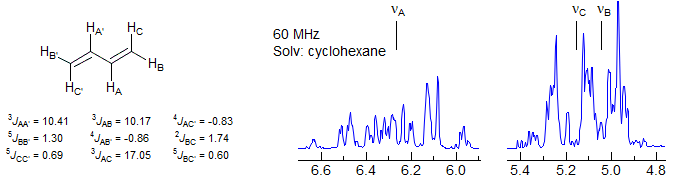
Analysis of Complex Spin Systems. In molecules where the chemical shift-equivalent protons are of the AA' type (part of an AA'XX', AA'X3X3' or similar system), complete analysis of the coupling system can, in favorable circumstances, give the value of JAA'. An example is 1,3-butadiene, an AA'BB'CC' system in which all protons are compled to all other ones. Analysis of the complex NMR spectrum gave, among numerous others, values for the following couplings between chemical shift equivalent nuclei: 3JAA', 5JBB' and 5JCC' (Hobgood, R. T., Jr.; Goldstein, J. H. J. Mol. Spectr. 1964, 12, 76).
Isotopic Substitution. Coupling between symmetry-equivalent protons can often not be measured directly. Replacing one of the protons by deuterium (or even tritium) breaks the symmetry of the coupled system and allows measurement of JHD (or JHT). The value of JHH can then be calculated from the gyromagnetic ratios. In the example below, the 60 MHz NMR spectrum of a mixture of undeuterated (s), monodeuterated (1:1:1 triplet, 2JHD = 2.58 Hz, the spin of D is 1, see Sect. 7-MULTI-2) and dideuterated (1:2:3:2:1 quintet) acetonitrile is shown. Note the upfield isotopic shift of 0.6 Hz per D (Grant, D. M.; Barfield, M. JACS 1961, 83, 4726).
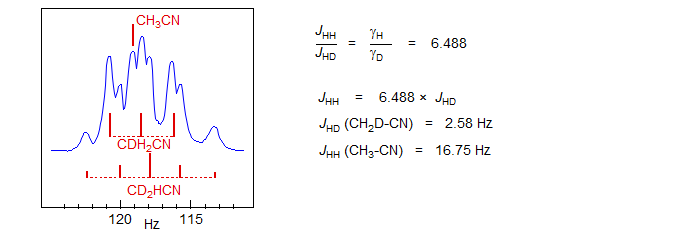
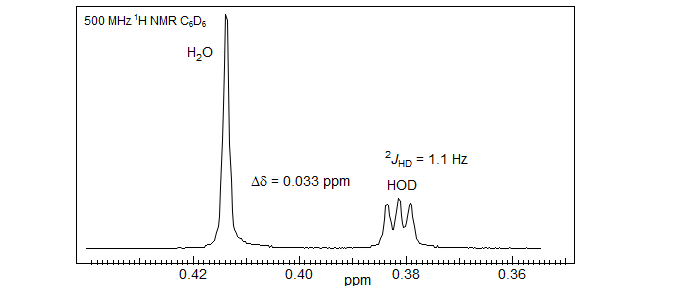
Another nice example of the use of D-labelling to determine coupling constants between equivalent protons is provided by the 500 MHz 1H NMR spectrum of a mixture of H2O and D2O in benzene-d6. The H2O peak is a singlet, the DOH a 1:1:1 triplet with 2JHD of 1.1 Hz, corresponding to 2JHH of 7.1 Hz (Glenn Facey, University of Ottawa, http://u-of-o-nmr-facility.blogspot.com/2008/10/.
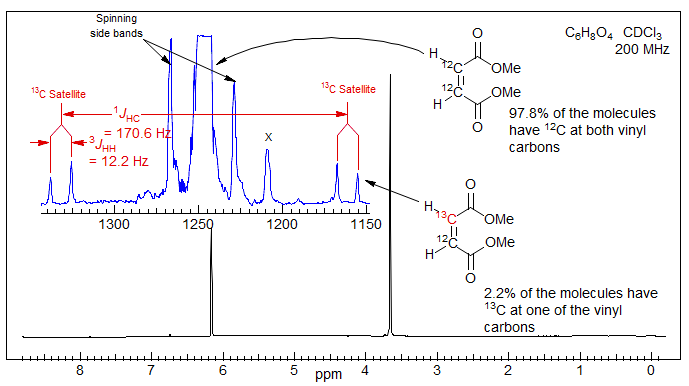
Analysis of 13C Satellite Spectra. Vicinal couplings between homotopic or enantiotopic protons 3JHH can often be obtained by analysis of the 13C satellites. The 1H NMR signal for the vinyl protons of dimethyl maleate is a singlet. However, the 13C satellites are doublets, with a splitting that is equal to 3JHH. In effect, the A2 spin system of the 12C isotopomer has become an ABX pattern in the mono-13C labelled compound, where X is the 13C nucleus, and A and B are the two vinyl protons, one on 13C and the other on 12C. Examples:, 1.
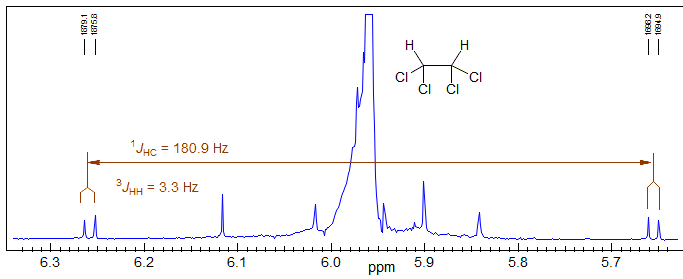
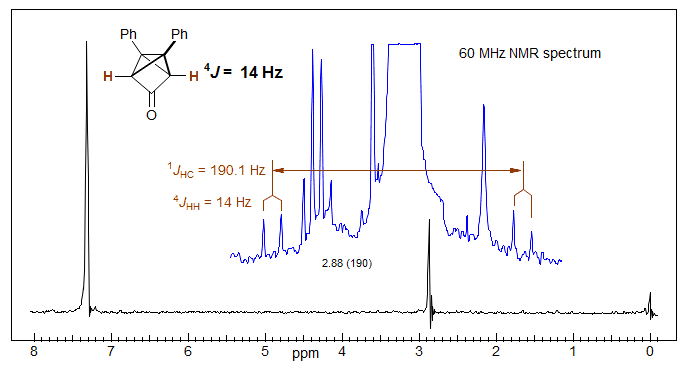
Below is an example of the measurement of a 4JHH in a symmetric tricyclic system using the 13C satellite method (Masamune, S. J. Am. Chem. Soc. 1964, 86, 735)
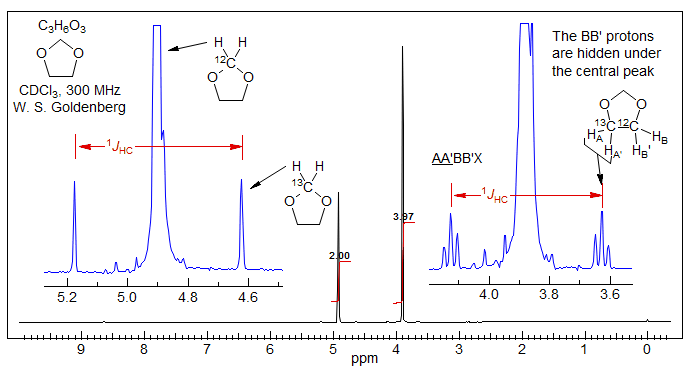
For systems of the X-CH2-CH2-X type, the mono-13C isotopomer is an AA'BB'X pattern (X = 13C), which can be solved to obtain JAA' (= JBB') as well as JAB and JAB'. Note that when both protons are on the same carbon the value 2J cannot be determined by this method. Thus for the O-CH2-O signal, the 13C satellites are singlets.
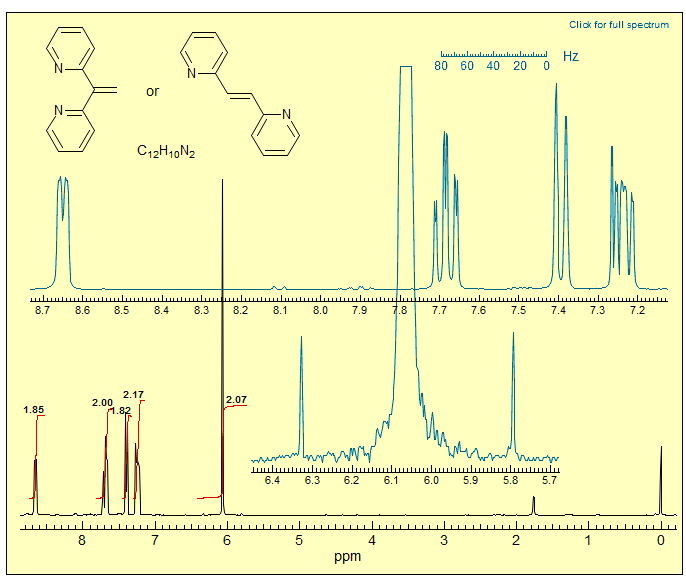
Exercise: The spectrum below could correspond to either the 1,1- or 1,2-bis(2-pyridyl)ethylene. Explain how the vertical expansion of the singlet at δ 6.06 allows a distinction to be made.
Next Section: Two-bond Coupling · Previous Section: Integration · Home