5-HMR-9 Second Order Effects in Coupled Systems
For first order systems J and δ values are directly measurable from line positions. However protons or groups of protons form first order multiplets only if the chemical shift differences between the protons (Δν) are large compared to the coupling constants between them (J), i.e. if Δν /J (all in Hz) is < 5 then second order effects appear. When Δν /J < 1 then second order effects become very pronounced, often preventing detailed manual interpretation of multiplets, or giving incorrect coupling constants if first order behavior is assumed.
There are a number of changes that occur in NMR spectra which are the result of degenerate or near-degenerate energy levels in strongly coupled systems i.e. when Δ /J becomes small (in English: whenever the coupling constant between two nuclei is similar in magnitude to the chemical shift between them, the spectra get complicated). If the spectrum is measured at higher spectrometer frequency the chemical shifts (in Hz) become larger, whereas the coupling constants stay the same, so the spectrum usually gets simpler. Exceptions are the AA'XX' type of systems, which are field independent, and usually cannot be completely solved from line positions and intensities alone.
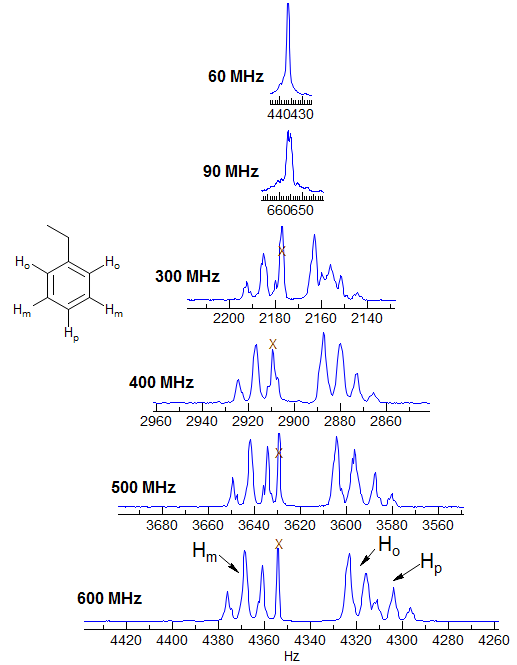
The effects of spectrometer field strength on the ability to resolve NMR coupling information is illustrated in this set of spectra of ethylbenzene, plotted at a constant Hz scale. The aromatic signals go from nearly a singlet at 60 MHz to a reasonably resolved set of peaks at 600 MHz (spectra courtesy of Kris Kolonko). This increase in information content and greater ease of interpretation of NMR spectra at higher magnetic field strength is the main justification for the additional expense of more powerful magnets.
We can define a hierarchy of coupling patterns which show increasingly larger number of second-order effects:
AX and all other first order systems (AX2, AMX, A3X2, etc.)
AB (line intensities start to lean, J can be measured, δ has to be calculated)
AB2 (extra lines, both J and δ have to be calculated)
ABX, ABX2, ABX3, JAB can be measured, others require a simple calculation
ABC (both J and δ can only be obtained by computer simulation)
AA'XX' (these do not become first order even at higher fields)
AA'BB'
AA'BB'X (etc)
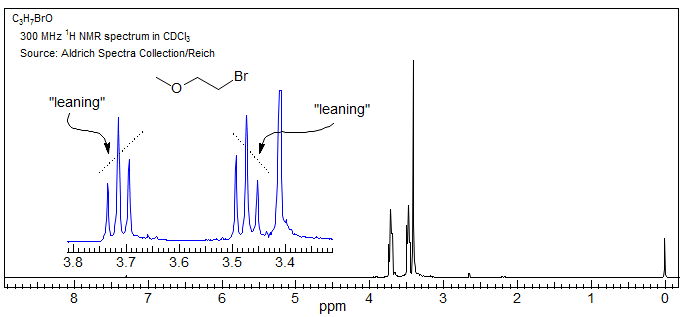
1. A universally observed effect is that as chemical shifts become comparable to couplings, line intensities are no longer integral ratios (AB and higher). The lines away from the chemical shift of the other proton (outer lines) become smaller and lines closer (inner lines) become larger (see the triplets below) - the multiplets "lean" towards each other (some call this a "roof" effect). The leaning becomes more pronounced as the chemical shift difference between the coupled multiplets becomes smaller.
2. Line positions are no longer symmetrically related to chemical shift positions (AB), eventually calculations may have to be carried out to obtain δ and J (AB2 and higher).
3. Some or all of the coupling constants can no longer be obtained from line separations (AB2 and higher).
4. The signs of coupling constants affect line positions and intensities (ABX and higher).
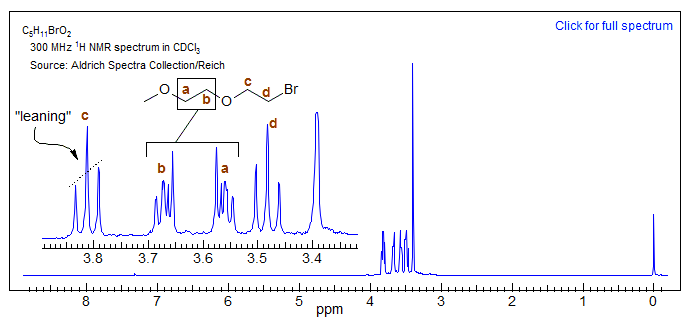
5. Additional lines over that predicted by simple coupling rules appear. First, lines which formally have intensities of 2 or more split into the component lines (e.g. the central peak of triplets). Eventually combination lines, which no longer can be assigned to any one nucleus appear (AB2 and higher). A nice example is provided by the compound below. For the BrCH2CH2O group the two methylenes at δ 3.48 and δ 3.81 (c and d) have a relatively large chemical shift separation, and they form recognizable triplets, although with a little leaning. For the MeOCH2CH2O group (a and b) the chemical shift between the CH2 groups is small, and the signals are a complicated multiplet with only a vague resemblance to a triplet. There is likely an additional complication from variability in the size of the two different vicinal couplings in the two patterns (see Section 5-HMR-15 for more on this). The additional lines can lead to "Virtual coupling" effects: apparent coupling to protons that are actually not coupled. See Section 5-HMR-16)
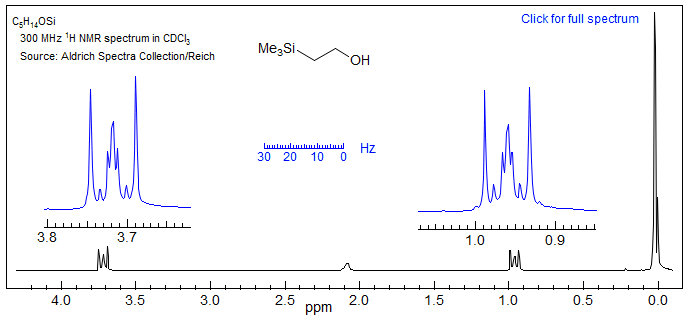
6. Coupling between equivalent nuclei (e.g., JAA' or JXX') affects line count and positions. Second order effects will appear even if Δν /J is large when groups of magnetically non-equivalent protons with identical chemical shifts are coupled to each other (see Section 5.8). Thus Me3Si-CH2-CH2-OH is not just two triplets, since the CH2CH2 is an AA'XX' system (see Section 5-HMR-14) These patterns do not get simpler at higher field strengths.
7. Computer analysis becomes mandatory to extract accurate J and δ values (ABC and higher). A typical example is the spectrum below, where a near coincidence of H1 and H2 leads to a complex spectrum. Even here one can make some sense of the multiplets - the one at δ 5.55 is H3, essentially a doublet of multiplets (J ≈ 10), at δ 5.72 another dm, with J ≈ 17 corresponding to H4. The peaks between 5.8 and 6.0 are H1 and H2, one can guess at some of the couplings from the downfield half of the H3 ddd, but this becomes quite risky.
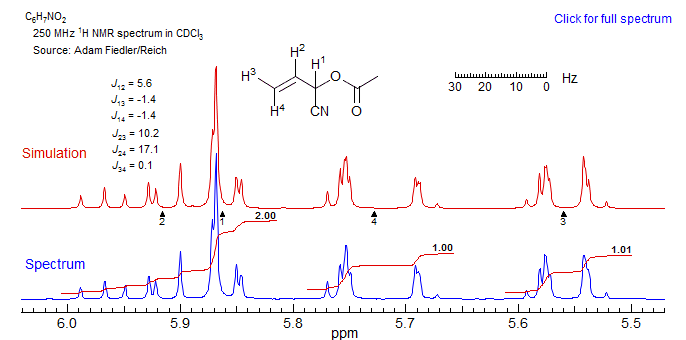
A computer simulation of this spectrum was performed with WINDNMR, and gave the simulated spectrum shown, using the J values indicated. To give some idea of what this involves, it took about 60 minutes of manual fiddling with the six J values and four δ values in WINDNMR to arrive at this simulation. Second order spectra like this are extremely sensitive to the parameter values - even a 0.1 Hz offset in several of the parameters significantly reduced the quality of the fit. Note that the chemical shift difference between H1 and H2 is 13.3 Hz, more than twice the value of the coupling between the two protons. The complexity is the result of the overlap between the upfield part of the H2 multiplet (which is over 30 Hz wide) and the downfield part of the H1 multiplet, which makes several of the energy levels degenerate, or nearly so.
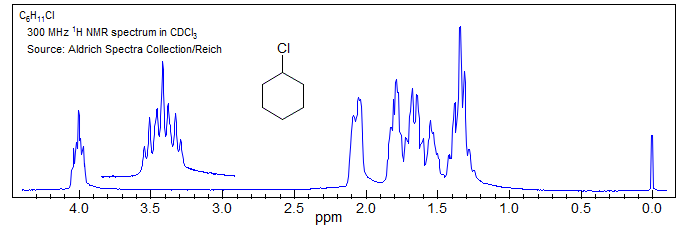
8. Ultimately spectra become so complex that the only useful information is integration, chemical shift and general appearance, as in the spectrum of cyclohexyl chloride, where only the proton α to the chlorine gives an interpretable multiplet (a tt), and even here the coupling constants obtained could be in error because of second order effects (possible virtual coupling).
Next Section: AX and AB Patterns · Previous Section: Symmetry · Home