5-HMR-10 AX and AB Spectra
The simplest molecules that show J coupling contain two spin 1/2 nuclei separated by 1, 2, 3 (occasionally 4 and 5) bonds from each other. If the chemical shift between the protons is large compared to the coupling between them (νAX >> JAX), we label them as HA and HX. If the chemical shift is comparable to the coupling between the protons (νAB < 5 JAX),we have an AB system. see NMR Gallery AB Spin system
5-HMR-10.1 Examples of AX and AB Spin Systems
Some molecules that give AB/AX patterns are shown below (spectra are all at 300 MHz):
· Disubstituted alkenes


· 1,2,3,4- and 1,2,3,5-tetrasubstituted benzenes; polysubstituted furans, thiophenes, pyridines, and other aromatic systems.

· Benzyl, methoxymethyl (MOM), benzyloxy-methyl (BOM) and related protecting groups in chiral molecules, and other isolated diastereotopic CH2 groups.
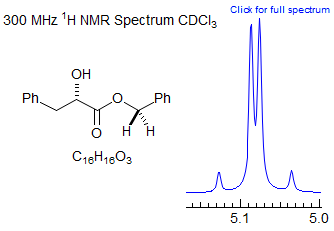
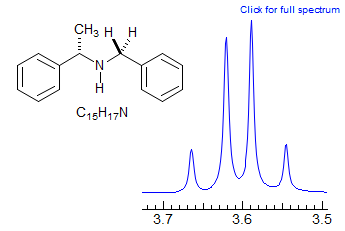
Exercise: Assign the protons in this partial 1H NMR spectrum.

Exercise: Assign the protons in this spectrum.

Exercise: Assign the protons in this spectrum.

5-HMR-10.2 Energy Levels of AX and AB Spectra
The four energy levels for an AX system are given in a very straightforward way by the equation below, by substituting the four possible spin combinations of mA and mX (++, +-, -+, --):
E = -(mAνA + mXνX) + mAmXJAX
There are four states: αα, αβ, βα, ββ. We will use the convention: αα is the lowest energy state (α is aligned with the field, m = +½) and ββ is the highest energy state (β is aligned against the field, m = -½). The first term in the equation is the chemical shift part, the second term the coupling part. If the coupling is a small perturbation, then the energy is simply the sum of the two parts. In energy level terms, this means that the energy separation of the αβ and βα states is large compared to J.


5-HMR-10.3 AB Spectra
When the energies of the αβ and βα states approach each other, they begin to mix, the αβ state develops some βα character and vice versa. Tthe mixing parameter Q specifies the degree of mixing - it approaches 0 as the chemical shift becomes large (no mixing) and approaches 1 as the chemical shift becomes very small (complete mixing). The energy of the βα state, instead of ½ (νA-νB), then becomes ½ [(νA-νB)2 + J2]½ (here defined as D)

In addition to these perturbations in energy levels, the probability of the transitions (i.e. line intensities) also varies - the A1 and B2 transitions become weaker and eventually disappear (i.e. they become forbidden), leaving only the A2 and B1 lines, which appear exactly at the chemical shifts of A and B when Δν becomes 0.



The distinction between an AB q and a regular q is not always trivial. In fact, if an AB quartet has the same Hz separation between the center two lines as the coupling constant J, then the intensities of the four lines are 1:3:3:1, exactly the same as for a regular q. Of course, an ABq must always integrate to at least 2 protons, and that may help with a distinction in this peculiar case.
Consider the multiplet below, which at first glance might be identified as a ddq. However, a proper analysis, which first removes the two smaller couplings, the dd, gives a child multiplet that does NOT have the correct line positions for a q (separation A is NOT the same as J, as required for a ddq). Rather, the intensities are those of an AB q, each line of which is split into a dd.

5-HMR-10.4 Solving an AB pattern:

Graphical method for determining the position of a leaning coupled partner. The point Q is the horizontal projection of the tip of line 2 on the position of line 1, and point P is the projection of the line 1 on the position of line 2. The line through P and Q intersects the baseline at the midpoint between the chemical shifts of A and B (point C) (https://www.ebyte.it/library/docs/kts/KTS isoAB Geometry.html). You can use this method to quickly estimate where a leaning doublet's coupling partner should be, if other peaks obscure the region of interest, or to determine whether you are looking at a leaning doublet, or two unrelated peaks. Example: for an assignment problem where an analysis of leaning provides crucial information see: 1.

Exercise: Are the two protons at δ 7.7 and 7.8 coupled to each other? Use the graphical method to show the coupling relationships, identify possible positions of the two substituents on the naphthalene, and assign the signals.

Exercise: The dibenzyl ester of aspartic acid salt has two different diastereotopic Ph-CH2 groups. Identify the peaks and calculate δAB and νAB for each.

It is not uncommon to see AB quartets with such a small νAB that the central lines are not resolved, even though the small outer lines are distinctly visible. An example is shown below (peaks centered at δ 3.43 corresonding to Ph CH2 protons). Such AB patterns cannot be accurately solved easily, but JAB will be just a little less than the separation between the small outer and central peaks. For another example in the context of an ABX system see this acrylamide spectrum.

Shown below is the 60 MHz spectrum of Abel's ketone in CDCl3 solution. There are three sets of protons that one would expect to form AB quartets. Exercise: Identify them on the structure.

The AB quartet at 3.7 δ can be analyzed as follows:

This is a little off because the intensity ratio is not very accurate, but allows proper assignment. You could also use the graphical method illustrated above.
Exercise: Why are the peak heights of the downfield doublet (ca δ 7.7) lower than those of the upfield one at δ 6.1? Hint: Section 5-HMR-06
5-HMR-10.5 How to report an AB quartet.
Journals require that NMR spectra be reported in text format. There are several ways an AB quartet could be reported:
1. Treat the pattern as first order (i.e., as two doublets). This is OK for AB quartets with a large νAB / JAB ratio, say > 4, where the error in chemical shifts caused by simply taking the middle of each doublet is small:
3.68 (d, 1H, J = 10.3 Hz), 3.79 (d, 1H, J = 10.3 Hz)
2. For closely spaced AB quartets (νAB / JAB < 4) the AB character should be explicitly shown, to indicate that the pattern was recognized, and the shifts were calculated correctly. One way is to report the two chemical shifts, and the coupling.
2.63, 2.69 (ABq, 2H, JAB = 12.2 Hz)
3. A third way is to report the chemical shift of the center of the AB quartet, and ΔδAB and JAB.
2.66 (ABq, 2H, ΔδAB = 0.05, JAB = 12.2 Hz)
Note that the latter two formats not only use less journal space but also contain more information than the "first order" format (1). There is nothing in the first description that specifies that the two doublets are coupled to each other, yet that would be obvious from observing the spectrum.
Exercise: The spectrum below is of four protons in the depsipeptide shown. Identify the protons, get δ and J.

Next Section: AB2 Patterns · Previous Section: Second Order · Home